Unbelievable Tips About What Is A Curve In Graph Theory Lucidchart New Line

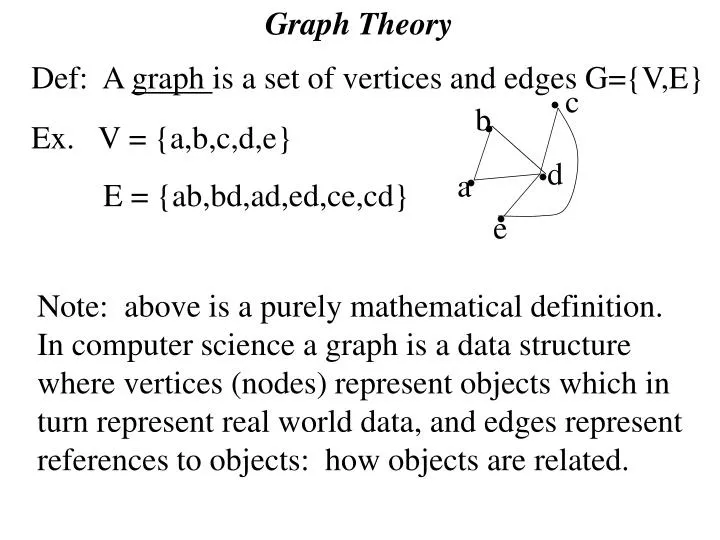
In the mathematical discipline of graph theory, a graph labeling is the assignment of labels, traditionally represented by integers, to edges and/or vertices of a graph.

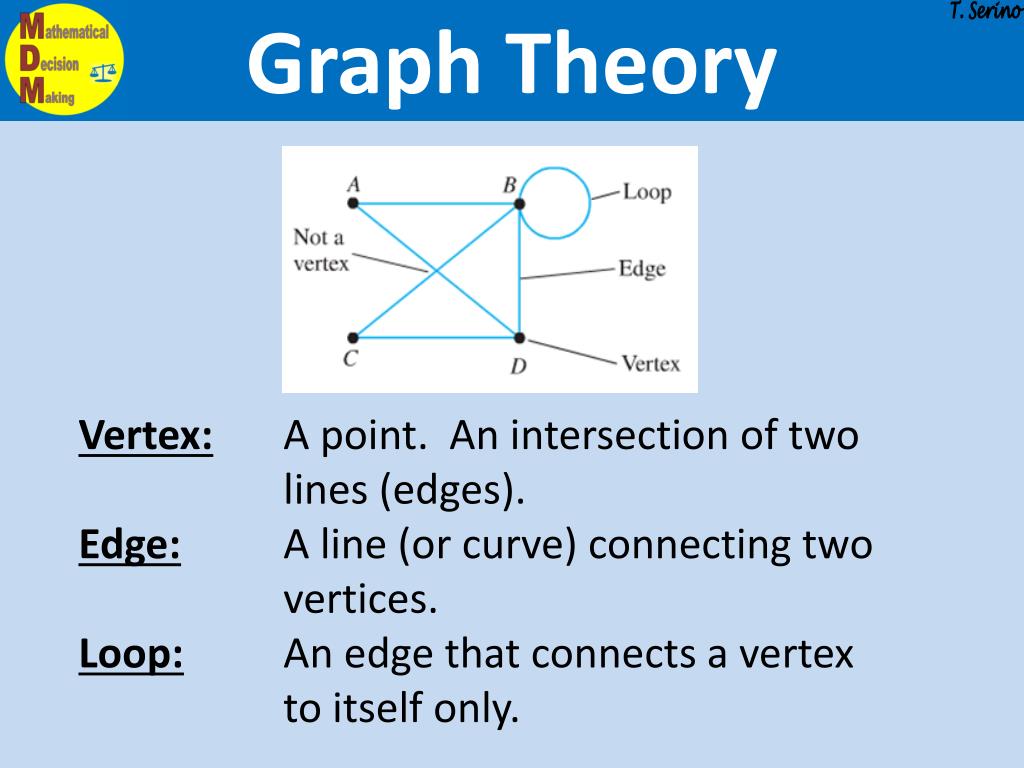
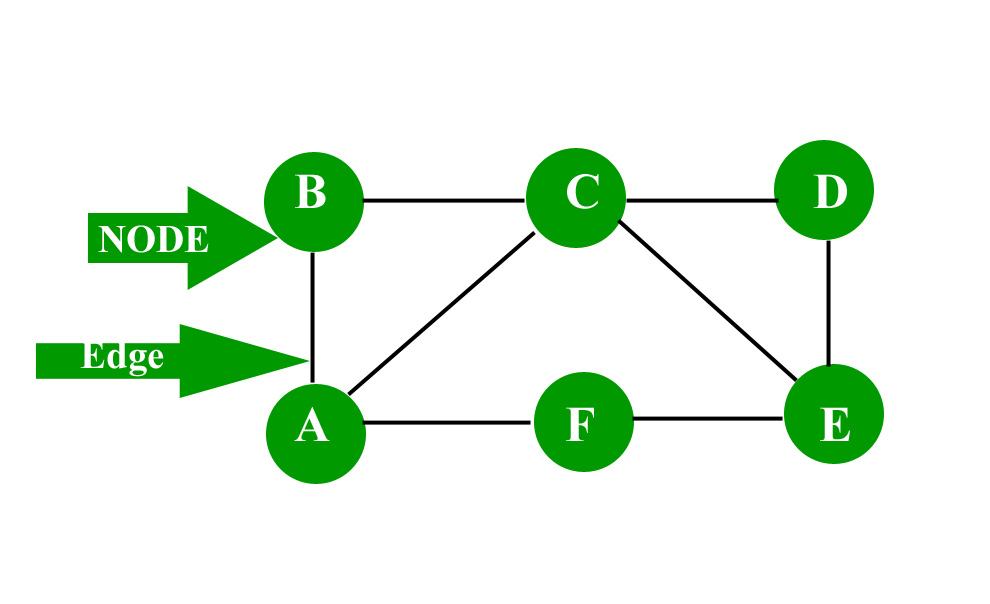
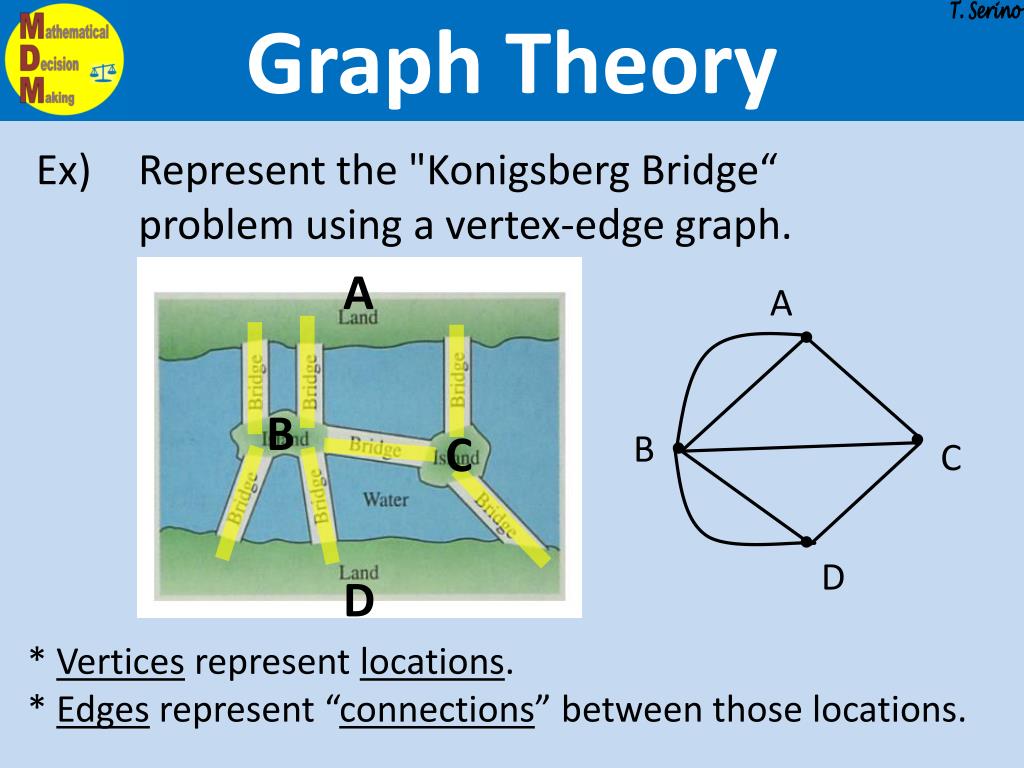
What is a curve in graph theory. The nominal trade deficit initially grows after a devaluation, as. The set v is called the set of vertices of g. A graph is depicted diagrammatically as a set of dots depicting vertices connected by lines or curves depicting edges.

\(v\), whose elements are referred to as the vertices of \(g\) (the singular of vertices is vertex); This is the jordan curve theorem. As the graph shifts to the left, the height of the graph has to increase in order to maintain the same area under the curve.

Formally, given a graph g = (v, e), a vertex labeling is a function of v to a set of labels; This connected components are what graph theorists call the faces of the embedding. Learn what a learning curve is, its models, formula, and how to calculate it.

The j curve is an economic theory that says the trade deficit will initially worsen after currency depreciation. We call e the set of edges of the graph g. The yield curve is a graphical representation of the interest rates on debt for a range of maturities.

Intuitively, a curve may be thought of as the trace left by a moving point. Sketching \ (f\) in example \ (\pageindex {1}\). How and where to apply it.

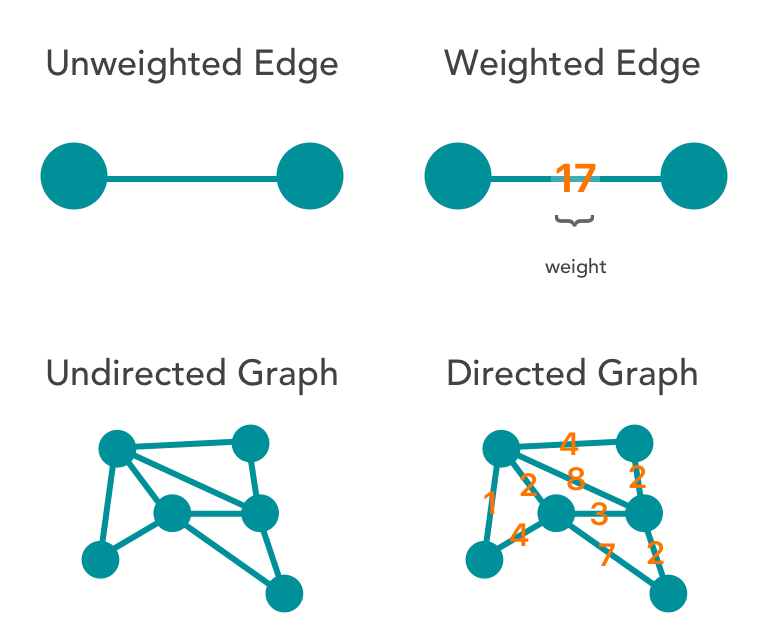
The elements of \(e\) are referred to as the edges of \(g\). A graph is a collection of vertices (also called nodes) connected by edges (also called links). With the aid of the jordan curve theorem, it is easy to show that either possibility necessarily results in at least one edge crossing.

The objects are represented by abstractions called vertices (also called nodes or points) and each of the related pairs of vertices is called an edge (also called. Given a graph g, g is a string graph if and only if there exists a set of curves, or strings, such that the graph having a vertex for each curve and an edge for each intersecting pair of curves is isomorphic to g. We start off with two interactive puzzles.

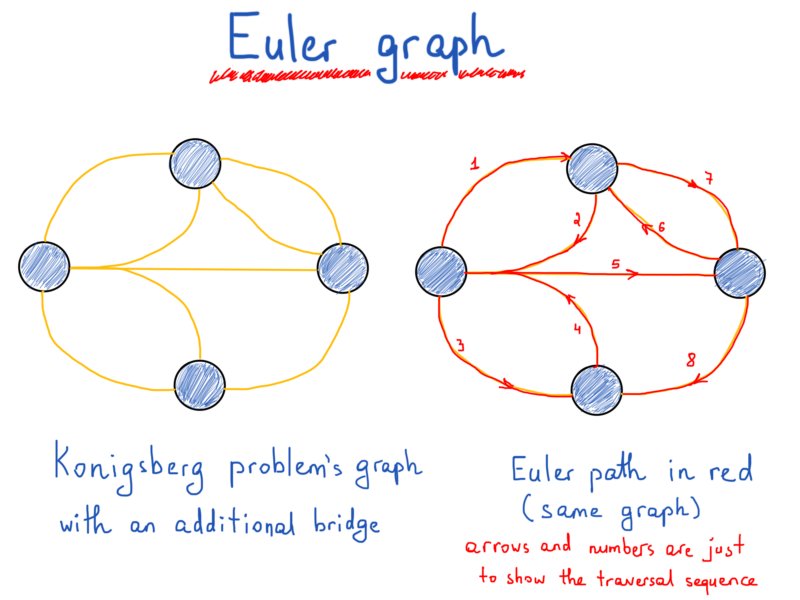
The proof then concludes that this shows that the $ug$ is nonplanar. In figure \ (\pageindex {2c}\) we show a graph of \ (f\) drawn with a computer program, verifying the accuracy of our sketch. A graph looks like this:

Graphs are used to model pairwise relations between objects, making them a powerful tool for representing and analyzing complex systems in various fields. It does not have any sharp turns. In my graph theory course, we are talking about planar graphs, and we studied the definition of a curve prior to talking about the jordan curve theorem.

In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight. The edges of a simple graph can be represented as a set of two element sets; Jordan curve theorem, in topology, a theorem, first proposed in 1887 by french mathematician camille jordan, that any simple closed curve—that is, a continuous closed curve that does not cross itself (now known as a jordan curve)—divides the plane into exactly two regions, one inside the curve and.