Have A Tips About Is There A Simple Graph Of The Degree Sequence 1 3 4 5 6 How To Add Line Bar

The degree 4 vertex must be adjacent to 0,.

Is there a simple graph of the degree sequence 1 3 3 4 5 6 6. The degree sequence is a graph. (we’ll stick to descending order. For a simple undirected graph with 5 vertices, the sum of the degrees must be even (since each edge contributes 2 to the total degree count).

The degree sequence of a graph g = (v;e) is just a list of the degrees of each vertex in v. Given a graph g = ( v, e) comprising a set of vertices v and edges e, the degree d ( v) of a vertex v ∈ v is the number of edges incident to v; When you're given a degree sequence, what is the method to draw a graph which has that degree sequence?

To avoid the temptation of looking for meaning in the order of the degree sequence, we typically list the degrees in sorted order. Note that a simple graph. The degree sequence of a simple graph is the sequence of the degrees of the nodes in the graph in decreasing order.

The degree sequence of a graph is a list of its degrees; The order does not matter, but usually we list the degrees in increasing or decreasing order. The degree sequence of a simple graph is the sequence of the degrees of the nodes in the graph in decreasing order.

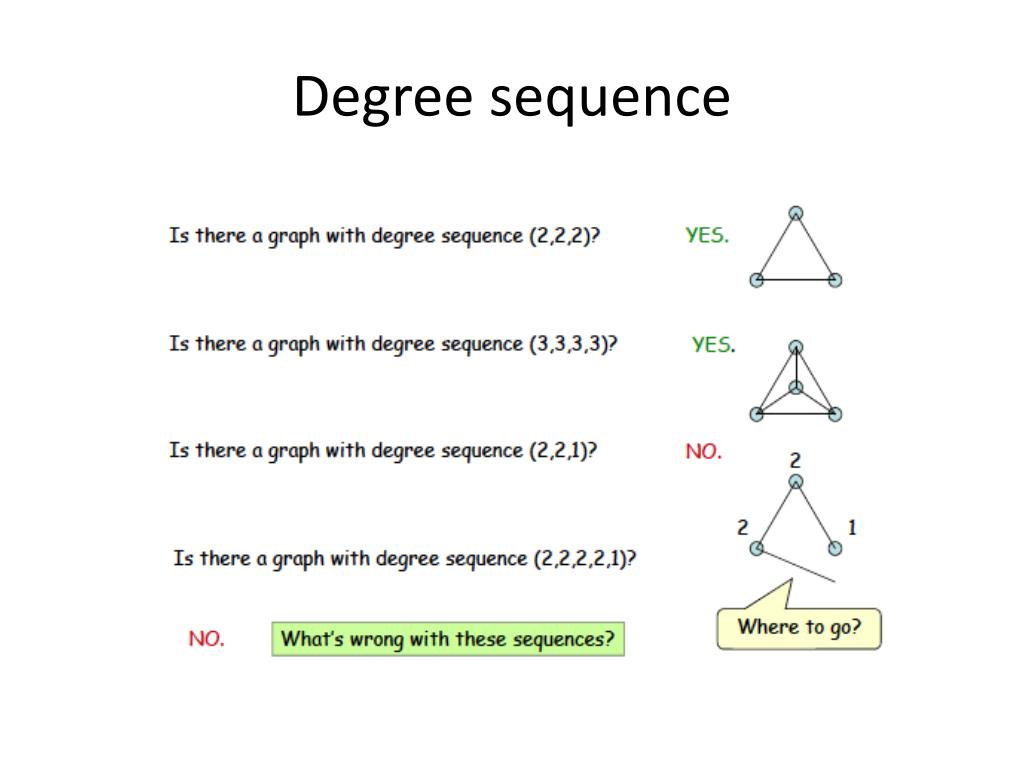
Then $g$ has the desired degree. 2vertices 1 and 3 are odd, while vertices 2 and 4 are even. The answer is false.

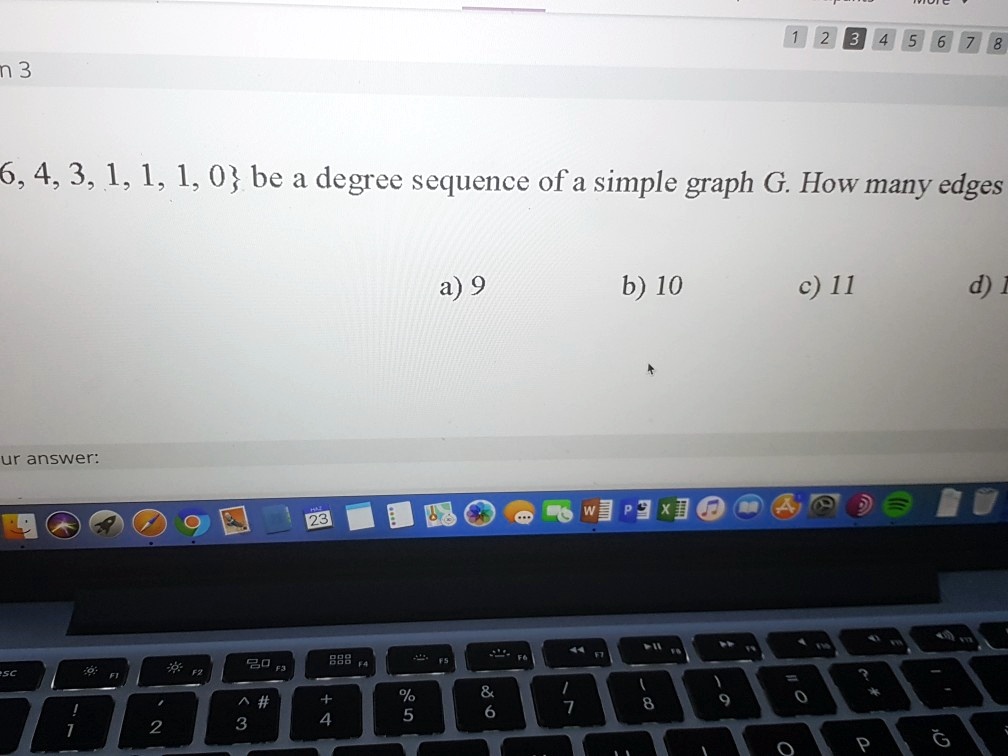
Which of the following sequences can not be. Degree sequence of a graph is the list of degree of all the vertices of the graph. The sequence (3, 3, 2, 1, 1, 0) (3, 3, 2, 1, 1, 0) is graphic.

Given an undirected graph, a degree sequence is a monotonic nonincreasing sequence of the vertex degrees (valencies) of its graph vertices. It is stated by wikipedia as: The degree sequence of a simple graph is the sequence of the degrees of the nodes in the graph in decreasing order.

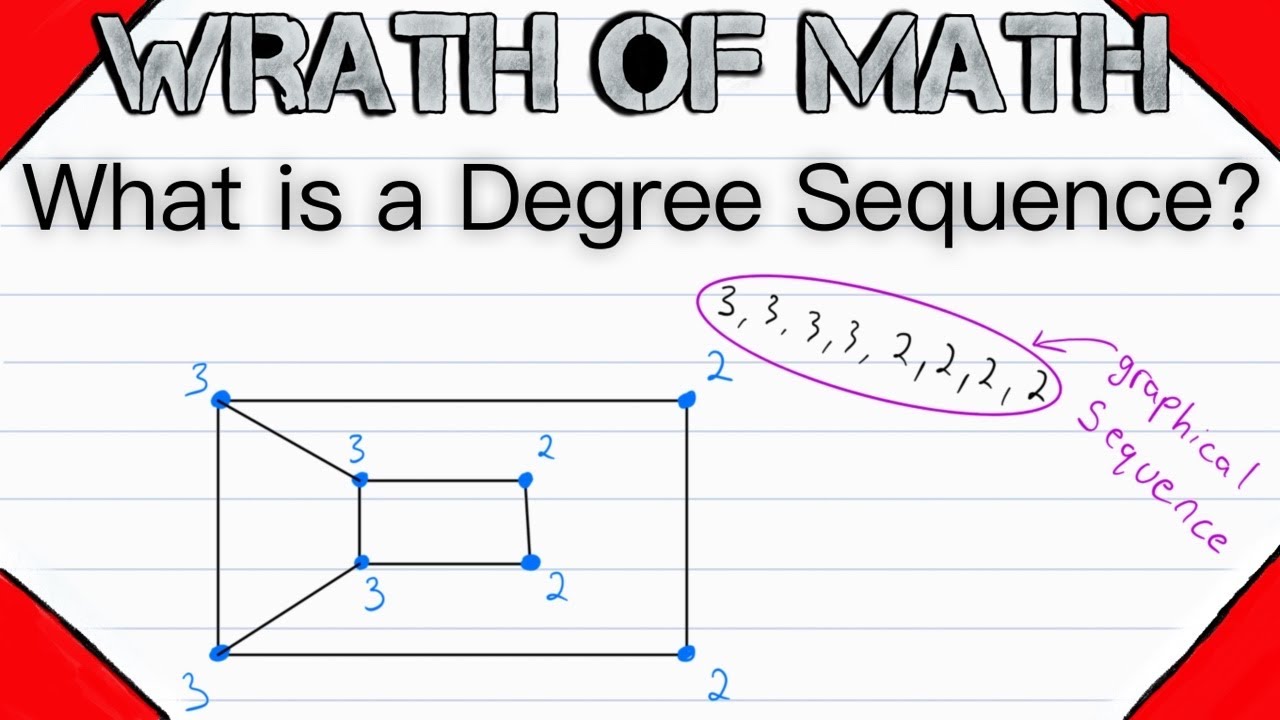
Degree sequence 2 example 0.1. For the above graph it is (5, 3, 3, 2, 2, 1, 0). Let g be a simple graph having degree sequence (1, 3, 3, 3,.

Which of the following sequences can not be the degree. Let $g$ be a graph with $v(g)=\{1,2,3,4,5\}$ and $e(g)=\{(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(3,4),(4,5)\}$. Degree sequence the degree sequence of a graph is the sequence of the degrees of the vertices, with these numbers put in ascending order, with repetitions as needed.

In the diagram, you can see the vertices have these numbers as their degrees. The theorem states that either all the following degree sequences can be realized as a simple graph or none of. Usually we list the degrees in nonincreasing order, that is from largest degree to smallest degree.