Ideal Info About Can You Have More Than One Line Of Best Fit Creating Chart In Excel With Multiple Data Series

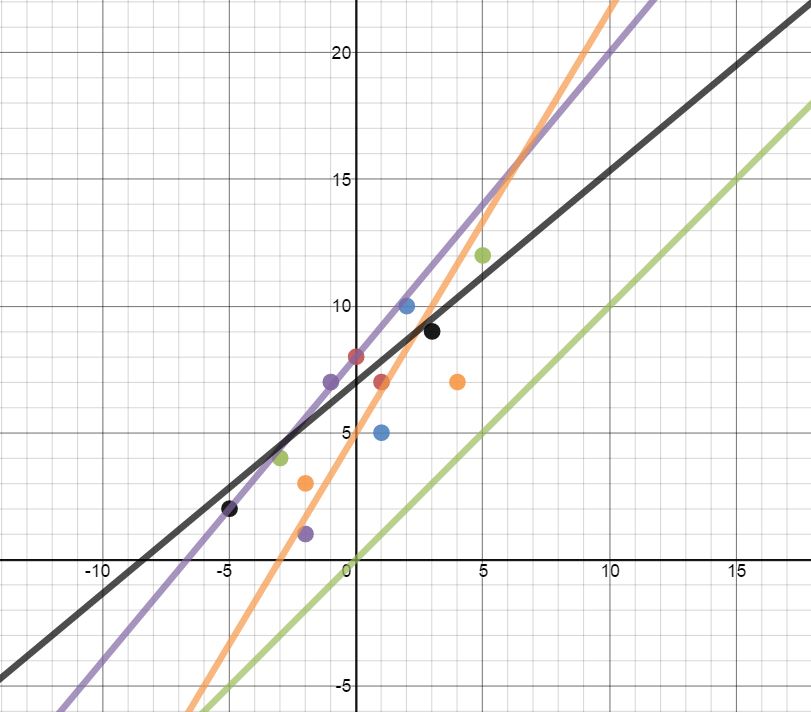
It is certainly possible (in mostly silly cases).
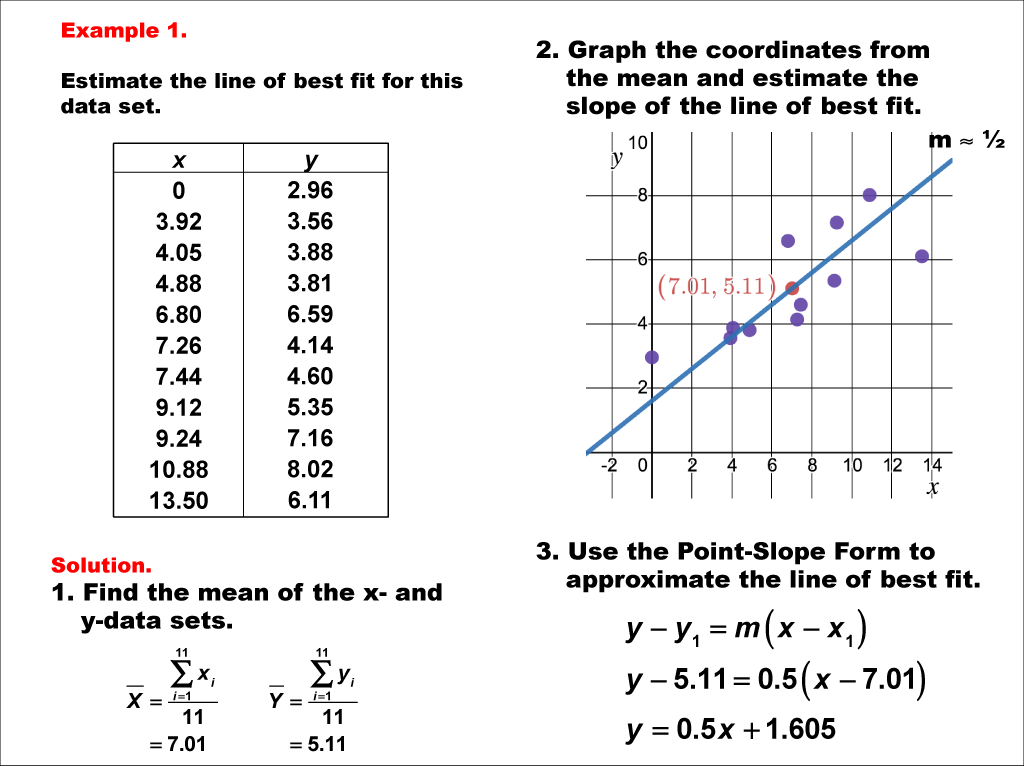
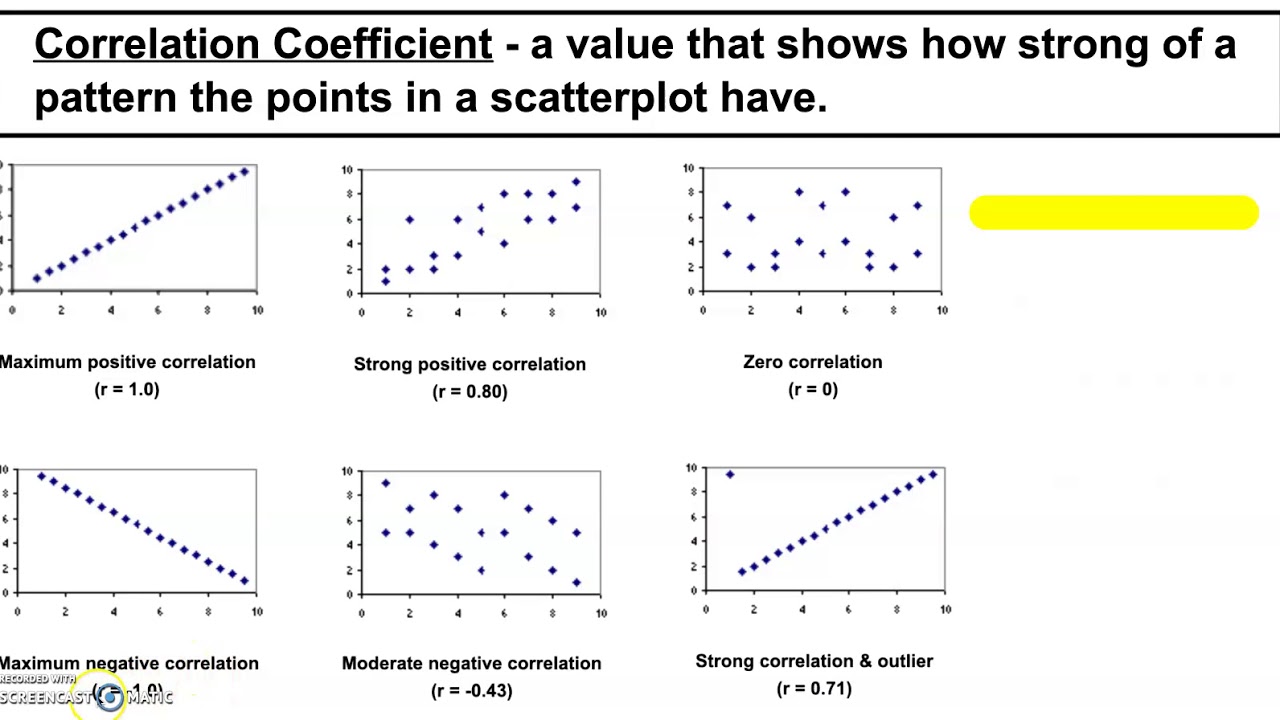
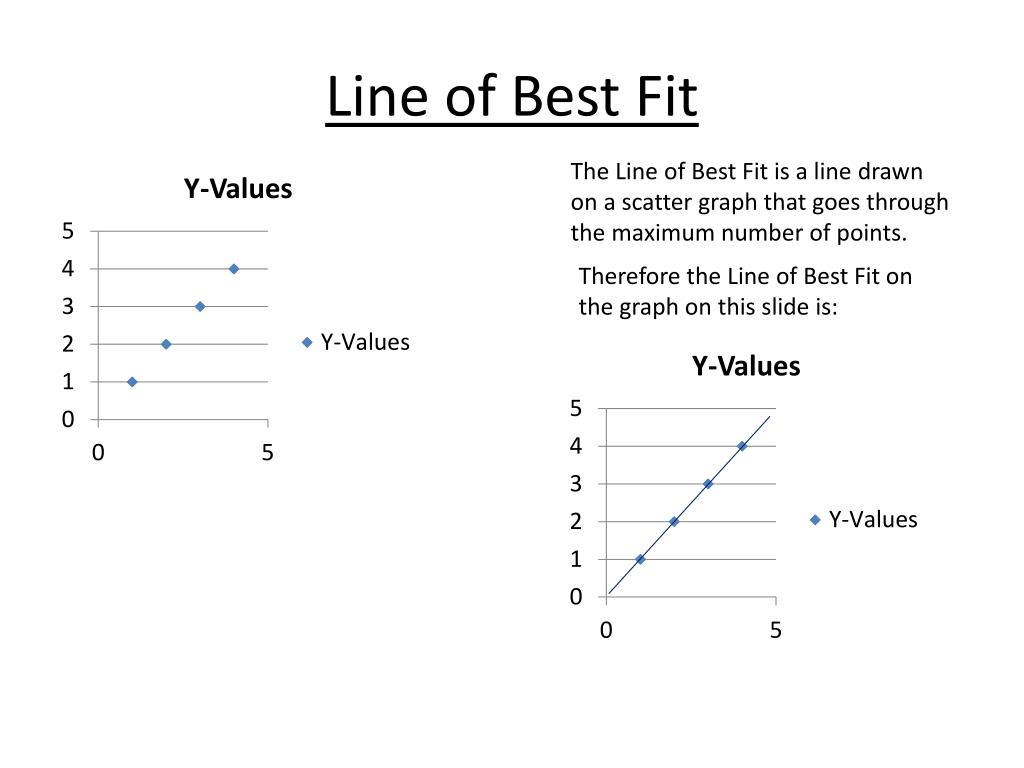
Can you have more than one line of best fit. A line of best fit is used to show a trend between points. Most scientists use a computer. The line of best fit for a scatterplot has the usual form of a line:
Core weakness can lead to fatigue, spine misalignment. Statistical software can calculate the equation for an 'ideal' line of best fit. We can use the line to make.
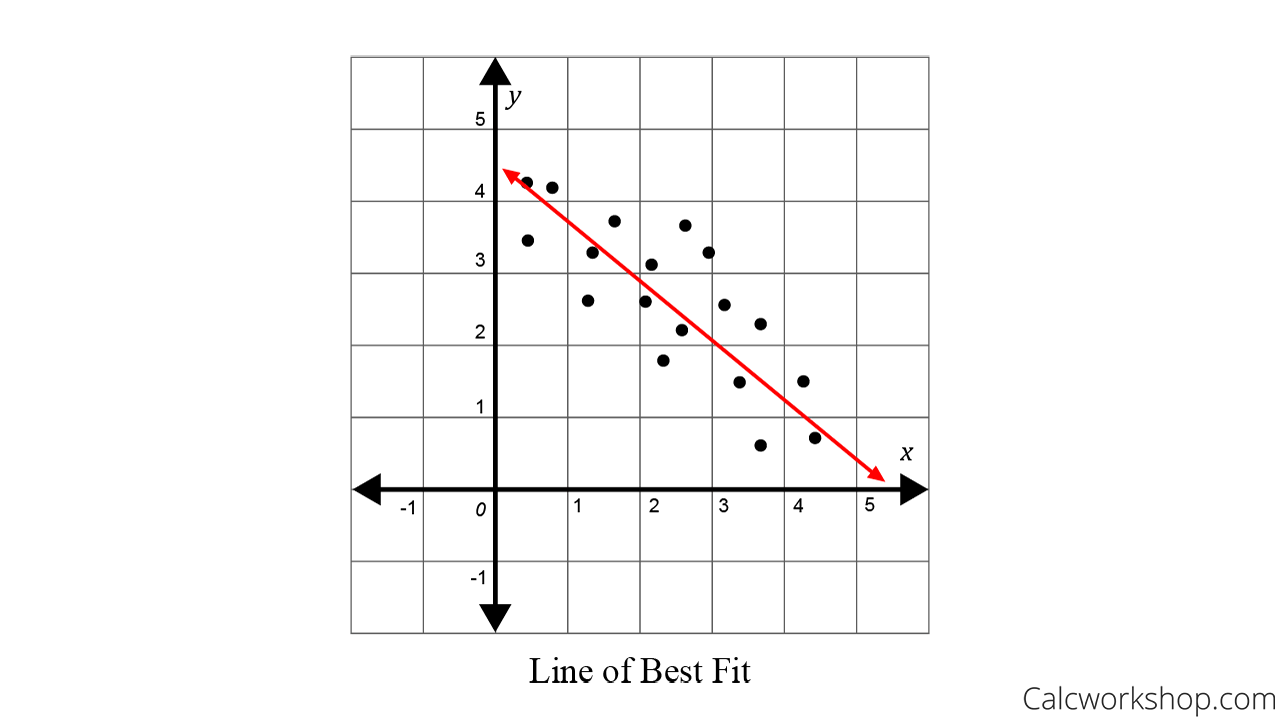
Is there a way to. Describing linear relationships with correlation; At the middle and high school levels, students are asked to determine a rough line of best fit by eyeballing a graph on the.
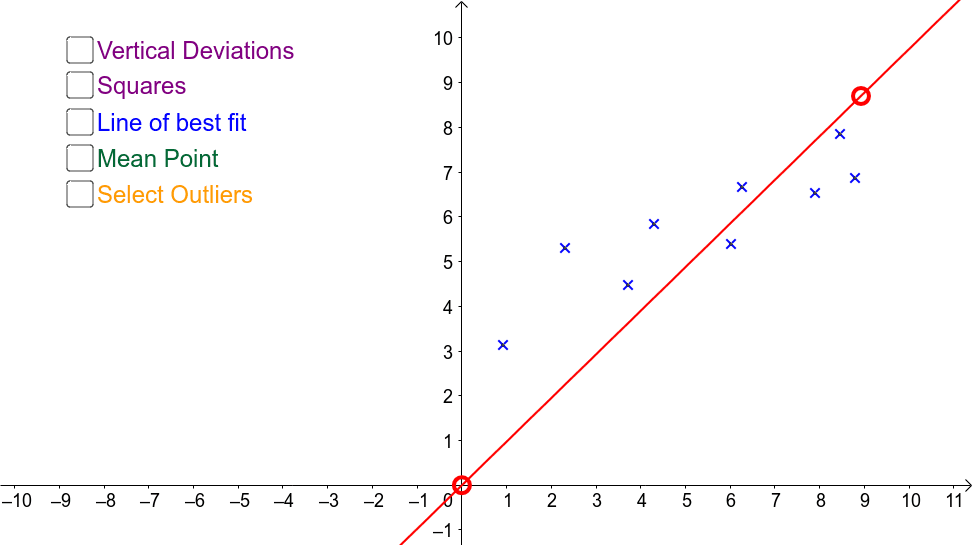
Walking can help strengthen the muscle groups that help stabilize the spine, primarily your core muscles. The criteria for the best fit line is that the sum of the squared errors (sse) is minimized, that is, made as small as possible. The line of best fit is studied at two different levels.
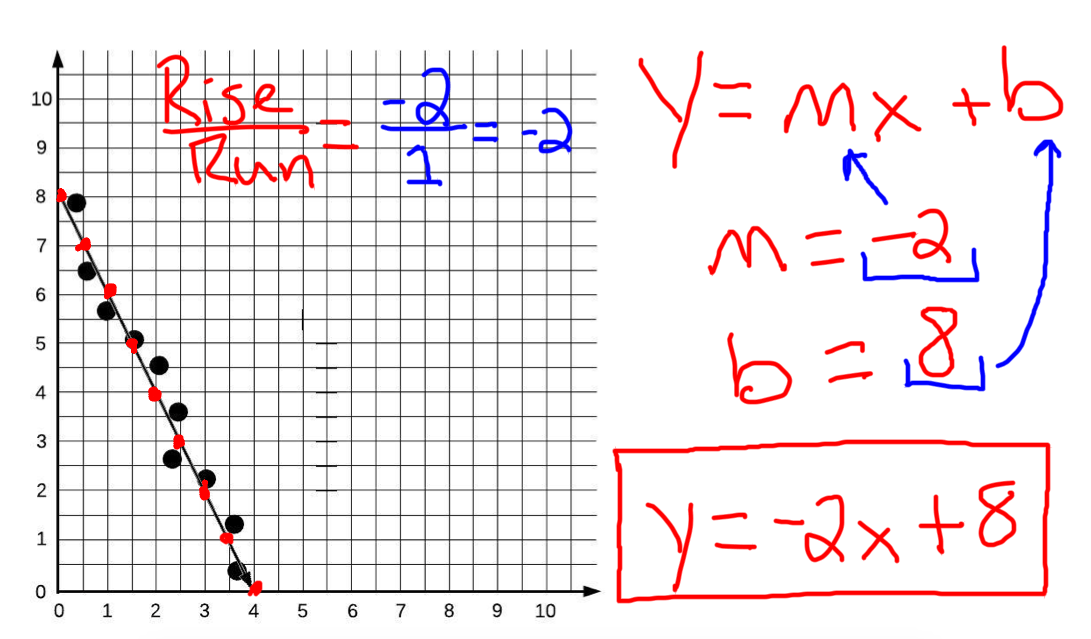
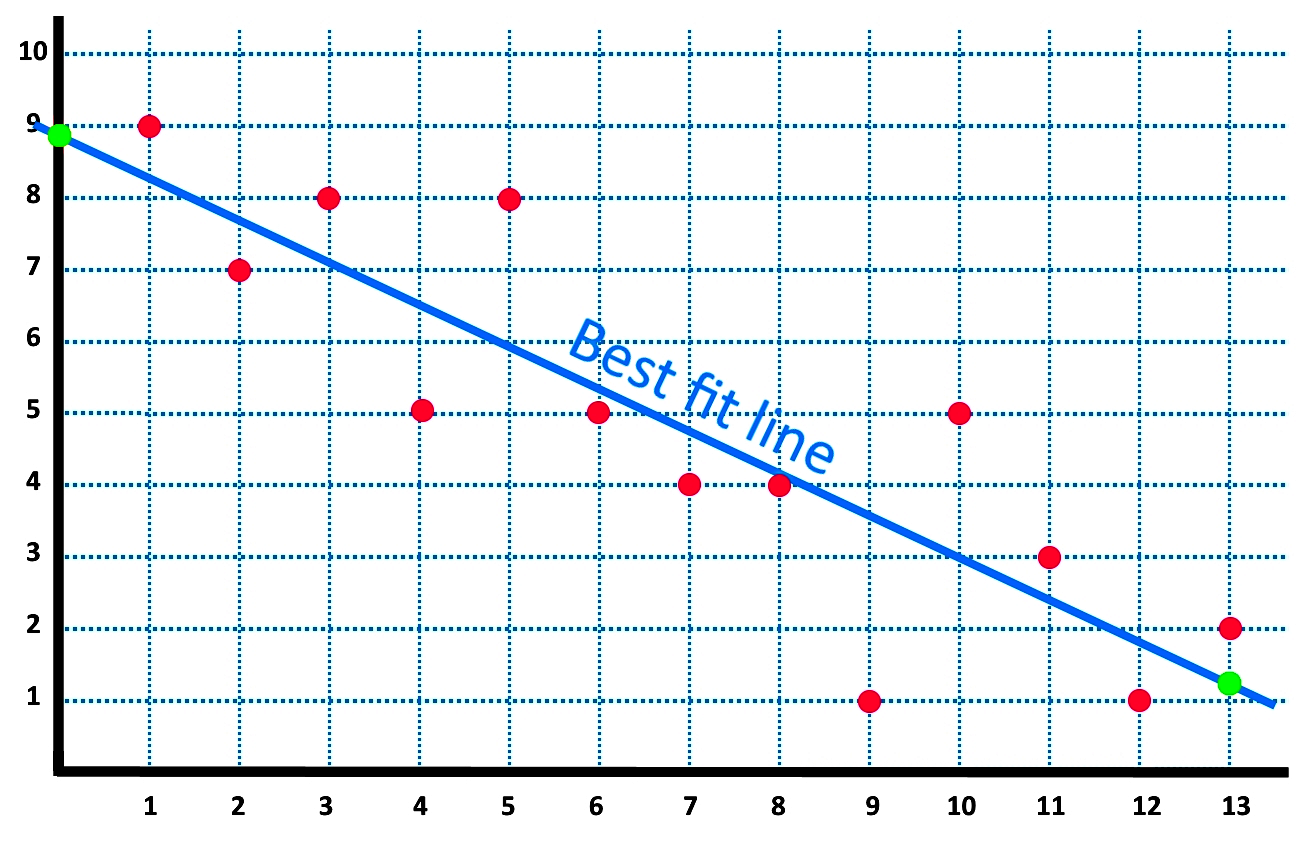
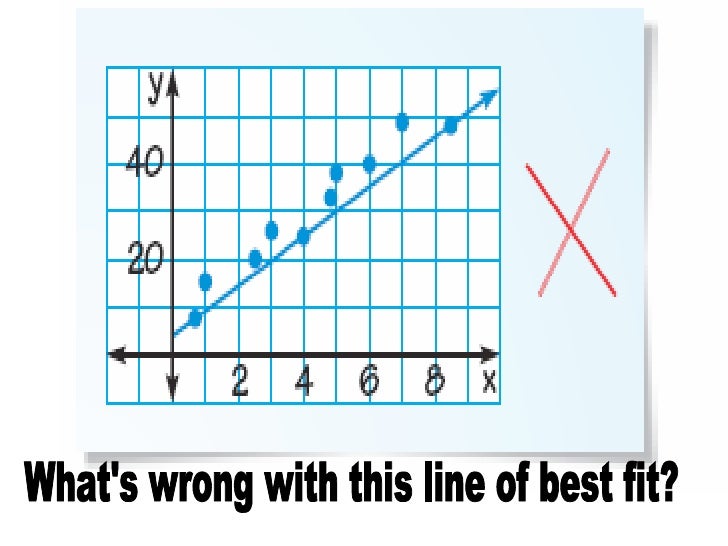
So the line of best fit in the figure corresponds to the direction of maximum uncorrelated variation, which is not necessarily the same as the regression line. The question is whether the line of best fit should be made to pass through the origin or not. The 'line of best fit' is a line that goes roughly through the middle of all the scatter points on a graph.
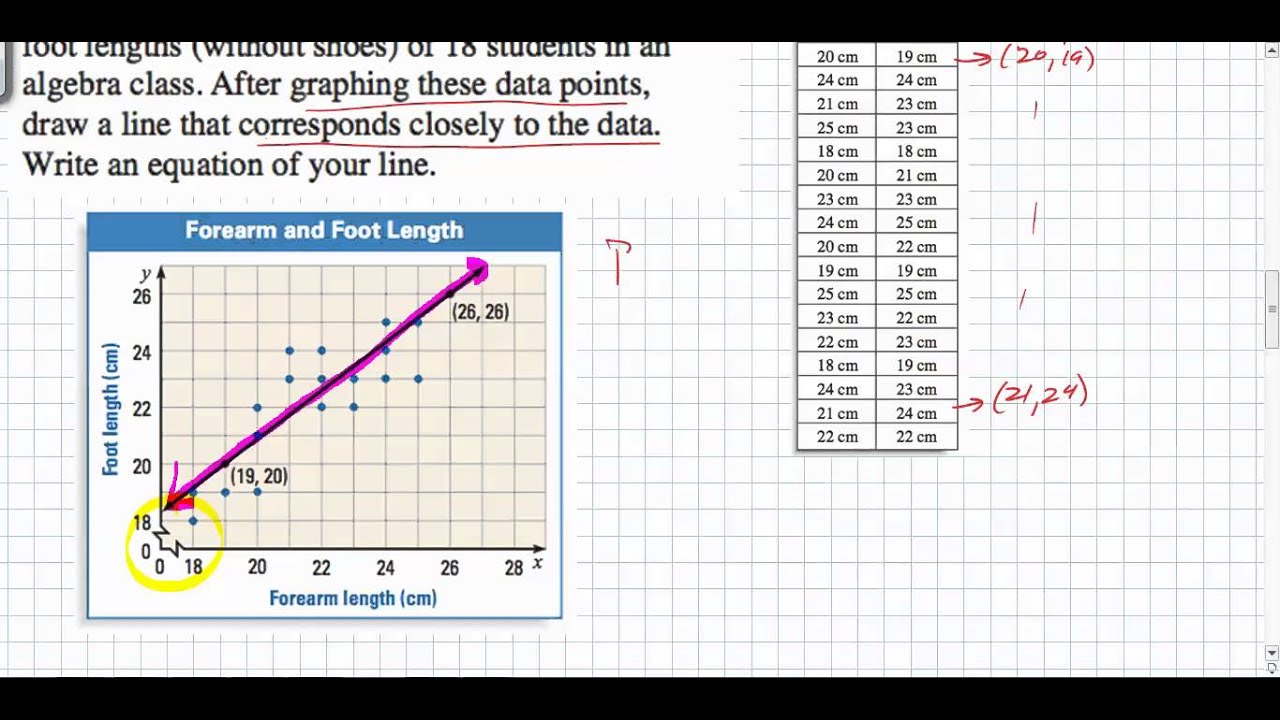
Predict the height of a person whose arm span is 190 cm, using the line of best fit given. In general, we fit lines to data when we want to use them for predictive purposes or to determine the general trend of the data. Using the graphing calculator to find the line of best fit.
Any other line you might choose would. 60 fl oz celebration ice cream cake, 40 fl oz strawberry. When gathering data in the real world, a plot of the data often reveals a “linear trend,” but the data don’t fall precisely on.
In the scatterplot pictured above, the line of best fit is y =. The line of best fit is given by the equation: Y = 0.95 x + 9.4.
Beginning with straight lines; We will also see examples in this chapter where. Remember that xk is your data for the independent variable.
Fitting a line by eye residuals; First recall that the linear best fit line is the line which minimizes the sum of squared residuals (see least squares): For example, suppose you sample the same x x value twice and get two experimental y y values that differ.





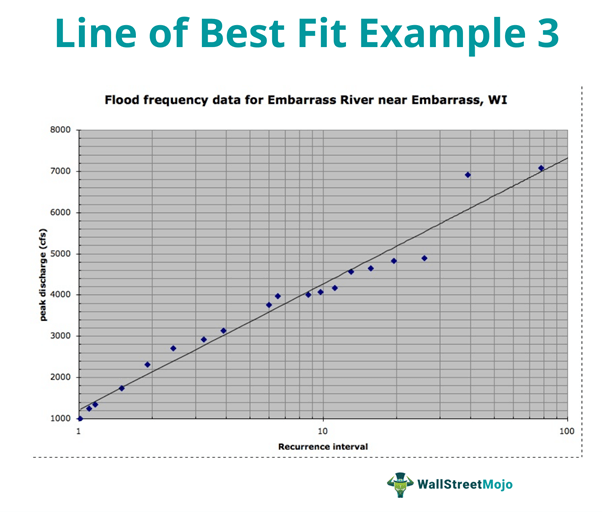

:max_bytes(150000):strip_icc()/Linalg_line_of_best_fit_running-15836f5df0894bdb987794cea87ee5f7.png)